la circunferencia: La definición de las funciones circulares

la circunferencia: La definición de las funciones circulares
http://bc.inter.edu/facultad/ntoro/TRIG2.htm

la circunferencia

A la distancia entre cualquiera de sus puntos y el centro se le denomina radio.

 El segmento de recta formado por dos radios alineados se llama diámetro. Es la mayor distancia posible entre dos puntos que pertenezcan a la circunferencia. La longitud del diámetro es el doble de la longitud del radio. La circunferencia sólo posee longitud. Se distingue del círculo en que éste es el lugar geométrico de los puntos contenidos en una circunferencia determinada; es decir, la circunferencia es el perímetro  del círculo cuya superficie contiene.

Puede ser considerada como una elipse de excentricidad  nula, o una elipse cuyos semiejes son iguales. También se puede describir como la sección, perpendicular al eje, de una superficie cónica  o cilíndrica, o como un polígono  de infinitos lados, cuya apotema coincide con su radio .

La circunferencia de centro en el origen de coordenadas y radio 1 se denomina circunferencia unidad o circunferencia goniométrica

ejemplo

Hallar la ecuación general de la circunferencia con centro C(2;6) y radio r = 4

(x - 2)² + (y - 6)² = 4²

x² - 2(2x) + 2² + y² - 2(6y) + 6² = 4²

x² - 4x + 4 + y² - 12y + 36 = 16

x² + y² - 4x - 12y + 4 + 36 - 16 =0

x² + y² - 4x - 12y + 24 = 0

D = -4 , E = -12 , F = +24

elementos de una circunferencia

Existen varios puntos, rectas y segmentos, singulares en la circunferencia:

• Centro, el punto interior equidistante de todos los puntos de la circunferencia;
• Radio, el segmento que une el centro con un punto cualquiera de la circunferencia;
• Diámetro, el mayor segmento que une dos puntos de la circunferencia (necesariamente pasa por el centro);
• Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros)
• Recta secante, la que corta a la circunferencia en dos puntos;
• Recta tangente, la que toca a la circunferencia en un sólo punto;
• Punto de tangencia, el de contacto de la recta tangente con la circunferencia;
• Arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia;
• Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro

Razones trigonométricas en la circunferencia unidad

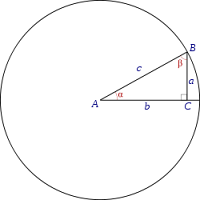
Si (x, y) es un punto de la circunferencia unidad, y el radio que tiene el origen en (0, 0), forma un ángulo con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triángulos rectángulos auxiliares, de la siguiente manera:

El seno es la razón entre el cateto opuesto (a) y la hipotenusa (c)

y dado que la hipotenusa es igual al radio, que tiene valor = 1, se deduce:

El coseno es la razón entre el cateto adyacente (b) y la hipotenusa (c)

y como la hipotenusa tiene valor = 1, se deduce:

La tangente es la razón entre el cateto opuesto y el adyacente

¿que es la Circunferencia goniométrica?

La circunferencia goniométrica, trigonométrica, unitaria o «círculo unidad» es una circunferencia de radio uno, normalmente con su centro en el origen (0, 0) de un sistema de coordenadas cartesianas, de un plano euclídeo.

Dicha circunferencia se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos auxiliares.

Si (x, y) es un punto de la circunferencia unidad del primer cuadrante, entonces x e y son las longitudes de los catetos de un triángulo rectángulo cuya hipotenusa tiene longitud 1. Aplicando el teorema de Pitágoras, x e y satisfacen la ecuación:

La definición de las funciones circulares

 Definición:

Que llamaremos:


sen a : “seno circular del ángulo a”, o, simplemente, “seno de a”
Función seno: f(x)= senx


cos a : “coseno circular del ángulo a”, o, simplemente, “coseno de a”
Función coseno: f(x)= cosx


tg a : “tangente circular del ángulo a”, o, simplemente, “tangente de a”
Función tangente: f(x)= tgx


ctg a : “cotangente circular del ángulo a”, o, simplemente, “cotangente de a”
Función cotangente: f(x)= ctgx (inversa de la tangente)


sec a : “secante circular del ángulo a”, o, simplemente, “secante de a”
Función secante: f(x)= secx (inversa del coseno)


cosec a : “cosecante circular del ángulo a”, o, simplemente, “cosecante de a”
Función cosecante: f(x)= cosecx (inversa del seno)